My crown jewels in Mathematics…
18 Mar 2023 (1131 Words, 7 Minutes)
NOTE : Link to the original post - is here
Nothing in mathematics is invented, one comes to the state of realization about existence of something which is already there, hence discovering it.
Mathematicians are fond of discovering patterns in numbers, shapes and geometry… and so are amateurs like me!
Here’s some basic terminology before we proceed -
My definition of Conjectures in mathematics: Its a guess which is based on a pattern, a conjecture (often) is a very difficult problem and it stands the test of time, meaning its very difficult to either prove it or disprove it. We also have a “counter-example” which disproves the conjecture, that’s where the pattern breaks. I believe that “explanation” to the behavior of patterns matters the most, and a valid explanation is called a proof. Once a conjecture is proven to be true, it becomes a theorem.
The proposition of such “guess” , based on the pattern which one identifies and then shares in the broader mathematics community, to either prove or disprove has almost always happened in a very rigorous way, like it comes from someone who is renowned or a prominent figure in mathematics community. So they proposed these “guesses” in their research articles, and then it was open to all the other mathematicians to work on it. Main thing is that it gets recognition from there, because your work is getting published in some reputed journal of mathematics, Meanwhile, there have been numerous amateurs too, who have proposed and proven significant conjectures in the past.
Here is the list of Conjectures in mathematics as of now I guess.
Also, see the List of unsolved problems in mathematics.
Its really hard to say when exactly a very difficult problem gains the status of a conjecture, but we can say it in a more appropriate way - consider the properties of conjecture again, only if it was easy to prove the existence of pattern till infinity, it would have become a theorem, or mere some problem which has a proof isn’t it Or if it had “counter-example” it would be a broken mathematical statement. But it ain’t easy!
Well, I wish you should consider Conjectures that have been disproved with extremely large counterexamples too. It happens. Also, Widely accepted mathematical results that were later shown to be wrong.
Motives behind this article —
It would come to my convenience to send the link to this article rather than emailing PDF individually, moreover I had never documented my works (I’ll say selected piece of work only) in a single place, which is open and accessible to all. Today I will document few of my conjectures in mathematics, (Number Theory - Prime Numbers) to be precise.
My level of knowledge while I was in the pursuit of discovering patterns in prime numbers was merely that of a High School graduate. I was a stubborn amateur, I was genuinely interested in prime numbers, and I attempted to study number theory the way it is established as of now, but I lost my motivation towards it, so I continued to do just my exploration, of a wild kind.
The outcome of my exploration was that I ended up discovering some beautiful and intriguing patterns in prime numbers, but again, all of it was a past and I am not working on it any further, however given an opportunity and I will consider picking up where I left, but more methodologically, rigorous and sound in the realm of mathematics.
Today, at the time of writing this article, I identify myself as an individual who is much involved in the Cybersecurity community and the Industry, practicing offensive security and operations. Please consider that if anyone wishes to progress on the works I have done, whether it be proving or disproving it, or just test it against the numerical evidences, feel free to do so, If possible keep me updated I will be more than happy, but do not expect me to delve deeper into these dimensions as of now. I don’t know number theory as its taught in the Mathematics textbooks, I know programming but I didn’t had courage to code and run tests against my so called Conjectures, meanwhile somebody who was interested did it, but a million is again a small number compared to the Infinity, that’s what my conjectures are up against.
Most importantly I wished to get this thing or rather urge to write an article about it, off my chest, and here we are.
Ingredients -
Calculator
List of prime numbers under 10,000
List of perfect squares and cubes of natural numbers
List of even numbers represented in a + b form
Plentiful of time, curiosity for finding patterns in prime numbers
So, among many of my conjectures, I picked up 11 of my best conjectures, and I used to email them to professors who specialized in the realm of number theory, however here, I will present only 7 of them.
Note: In the 4 consequent conjectures below, gcd(a,b) = 1 constraint is not applicable. I have forgot to remove that
Conjecture 1 : (Generalized Goldbach’s Conjecture)
Goldbach’s Conjecture reference : “Goldbach’s conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even whole number greater than 2 is the sum of two prime numbers.”
some 280 years old unsolved problem, however there have been progress to prove it, but I won’t mention it all here.
I never really attempted to generalize Goldbach’s Conjecture, but its just another beautiful pattern which I discovered while exploring the realm of prime numbers.

We can derive Goldbach’s Conjecture, however reworded as -
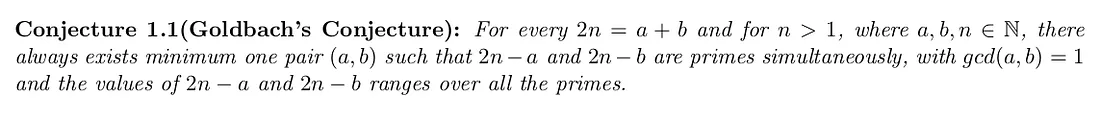
The beauty is, the expressions being primes simultaneously. In similar fashion and spirit, we have -

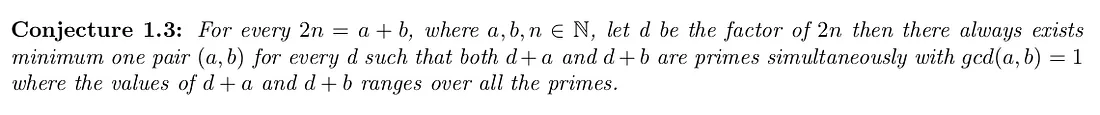
Conjecture 2-3 : Mystery of common exceptions
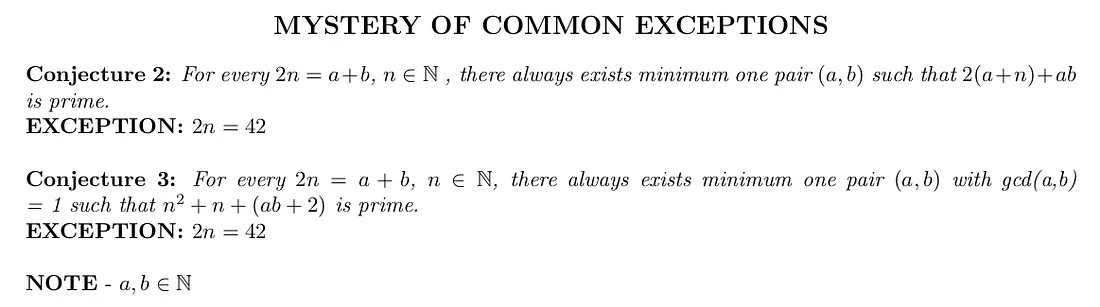
When I found the second expression while I was playing with various prototypes of polynomials, I was shocked, I never expected that I’ll find any other similar expression which holds 2n = 42 as an exception. Its weird, beautiful, and I really wish that someone could explain this behavior, and even more interestingly, I’ll await another such expression which holds 2n = 42 as an exception or who knows there could be infinity of such!
Conjecture 4 : Realm of Squares, Cubes, Primes…

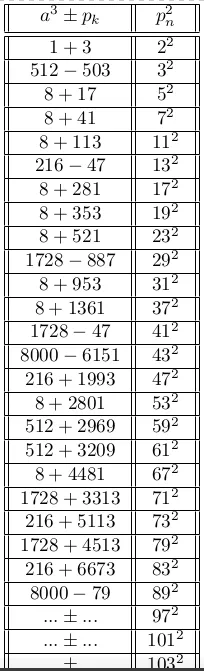
Conjecture 5 :

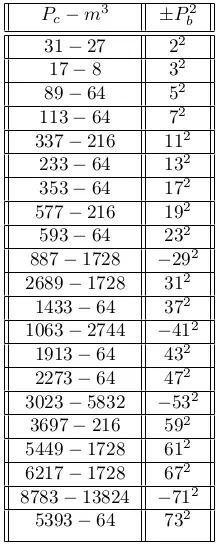
These numerical evidences are small in number, and I did it with calculator, however using heavy computational resources we can test its validity for much large numbers, and with a valid explanation / proof, till infinity.
Conjecture 6 :
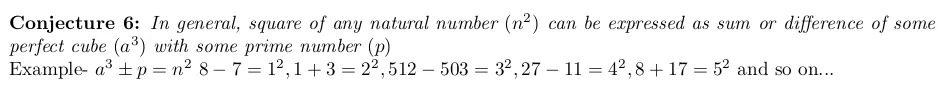
Conjecture 7 :

As the value of “n” increases, we could have more possibilities of similar permutations, I find it beautiful.
Bonus Conjecture xD

Some of these might take some efforts to understand and get hold of the pattern, but eventually its all beautiful prime numbers.
As of now, this is all I have to show. Finding patterns in prime numbers was difficult, but I enjoyed it a lot, I wish I could do it again.
For contacts, here’s my Twitter handle, or drop it in the comments section.
Mathematics is the language of Universe. Much respect to all of the Mathematicians, may Mathematics progress to address these conjectures before I die lmao, … Before I die I really wanna see either counter-examples, or some heavy numerical evidences supporting these pattern, or maybe proofs/disproofs! who knows.