I used ChatGPT-4 to test my Conjectures!
19 Mar 2023 (5756 Words, 32 Minutes)
It’s been almost an year ever since I had posted my conjectures online, consolidated in a single place. Today I am gonna report some significant progress on them - via computational evidences, python scripts which one can run on their machines to test these conjectures and some more exciting conjectures and prototypes!
NOTE : This is the previous blog I am referring to throughout this post
Since previous compilation of conjecture was handpicked, this one has some more gems to offer. It’s highly recommended to read my previous blog post before continuing with this one.
I have harnessed the power of ChatGPT-4 extensively to test these conjectures. GPT-3 and 3.5 were not so good with handling complex instructions and requirements to form the logic for rigorous scripts, but GPT-4 exceeded my expectations.
Prime Amplifying Sniper
To begin with today’s revelation, I would like to walk you through some fantasies. Being an amateur I have plenty of them when it comes to prime numbers. Think about - a polynomial which takes smaller inputs and yields bigger primes? and that too being cost-effective?!
Suppose there’s a magic box, you posses a red colored ball but your heart always longed for yellow ones, now that magic box takes your input (red colored ball) and yields a finite set of other balls - out of which is almost guaranteed to have a minimum of 1 yellow colored ball. Think about it.
Well, it’s right here, and I believe there are infinite of them. I had generalized those polynomials as well, but that would make for some other blog post.
I was looking into my old conjectures, out of which I found some more gems to offer today. Consider this conjecture -
For every \(2n = a + b\) where \(n \in N\), there always exists minimum one pair \((a,b)\) with \(gcd(a,b)=1\) such that \(a^3b + nk\) is prime for \(0 < k \leq 2\), \(k \in N\).
Consider the natural number n, once you have picked it’s value, you partition \(2n\) in the form of \(a + b\), then ensure \(gcd(a,b) =1\) and then plug it in the expression \(a^3b + nk\) where \(k\) is either 1 or 2.
By the grace of ChatGPT-4, I had a python script by my side which outputs the highest prime yielded by any given value of \(n\), and that too in a tabular manner.
Here’s the script to test this conjecture -
#!/usr/bin/python3
import math
from tabulate import tabulate
def is_prime(num):
if num <= 1:
return False
for i in range(2, int(math.sqrt(num)) + 1):
if num % i == 0:
return False
return True
def gcd(a, b):
while b:
a, b = b, a % b
return a
def test_conjecture(n, limit=1000):
highest_prime = 0
for a in range(1, limit + 1):
b = 2 * n - a
if gcd(a, b) == 1:
for k in [1, 2]:
expr = a**3 * b + n * k
if is_prime(expr) and expr > highest_prime:
highest_prime = expr
return highest_prime
if __name__ == "__main__":
start_n = int(input("Enter the starting value of n: "))
end_n = int(input("Enter the ending value of n: "))
n_values = list(range(start_n, end_n + 1))
highest_primes = [test_conjecture(n) for n in n_values]
times_bigger = [round(highest_prime / n, 3) if highest_prime > 0 else 0 for n, highest_prime in zip(n_values, highest_primes)]
table_data = list(zip(n_values, highest_primes, times_bigger))
headers = ["n", "Highest Prime", "Times Bigger"]
print(tabulate(table_data, headers=headers, tablefmt="grid"))
Please ensure that your system meets the dependencies to run the script.
This is how the output looks like once you save the script with .py extension, giving it sufficient executable permissions and running it.
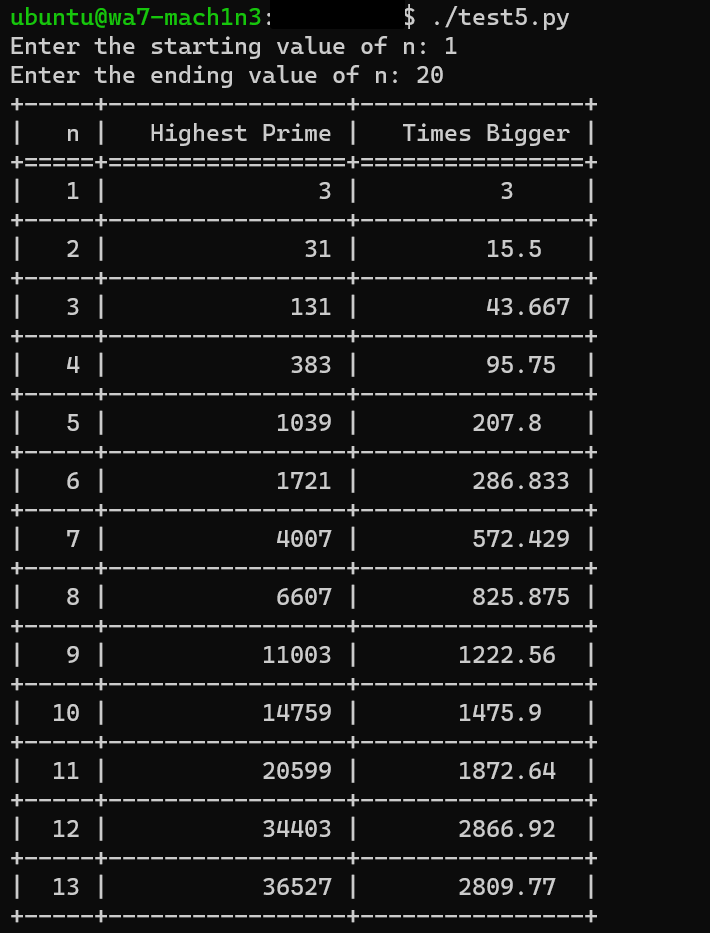
Now you might be curious how fast it grows over time and the value of \(n\) increases, it yields much bigger primes. Tables won’t do much justice, so we’ll look into graphs now -
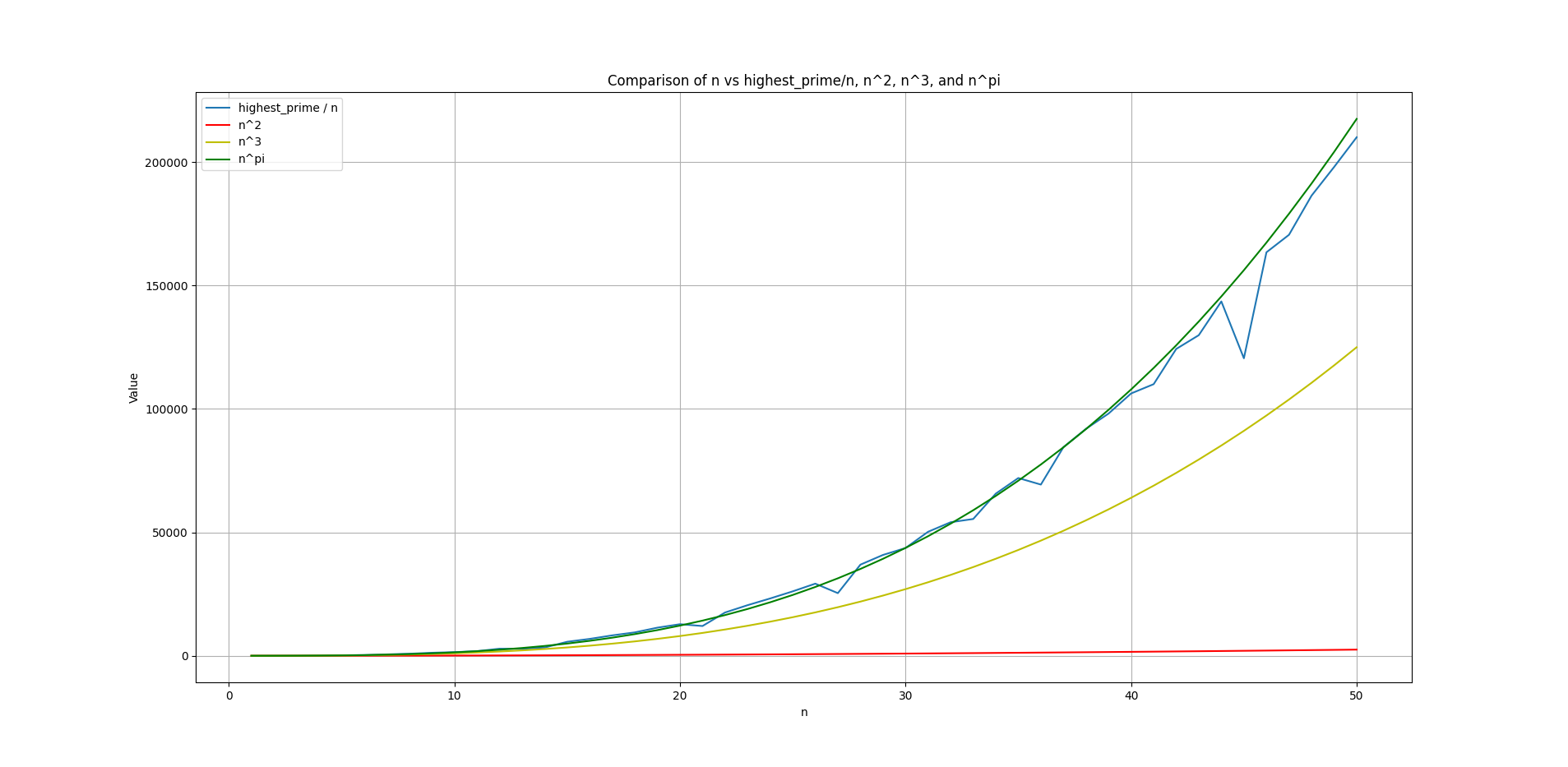
Plotted for \(n = 1\) to \(n = 50\). It takes some smaller dips over time as n grows, but it is consistently increasing. On the \(x\) axis we have the value of \(n\) and on \(y\) axis we have the “value” which is basically the highest_prime / n. It’s been rounded off to nearest numbers. For instance, when \(n = 50\), the prime it yields is 10503509 which is 210070 times bigger than its input i.e., 50. And evidently this graph shows us how fast it grows, it touches just over 2,00,000.
I have incorporated the curve of \(n ^ \pi\), along with \(n ^2\) and \(n^ 3\). It was simply because I was tweaking the curves to see which one aligns well with it. However, it separates as the value of \(n\) grows -
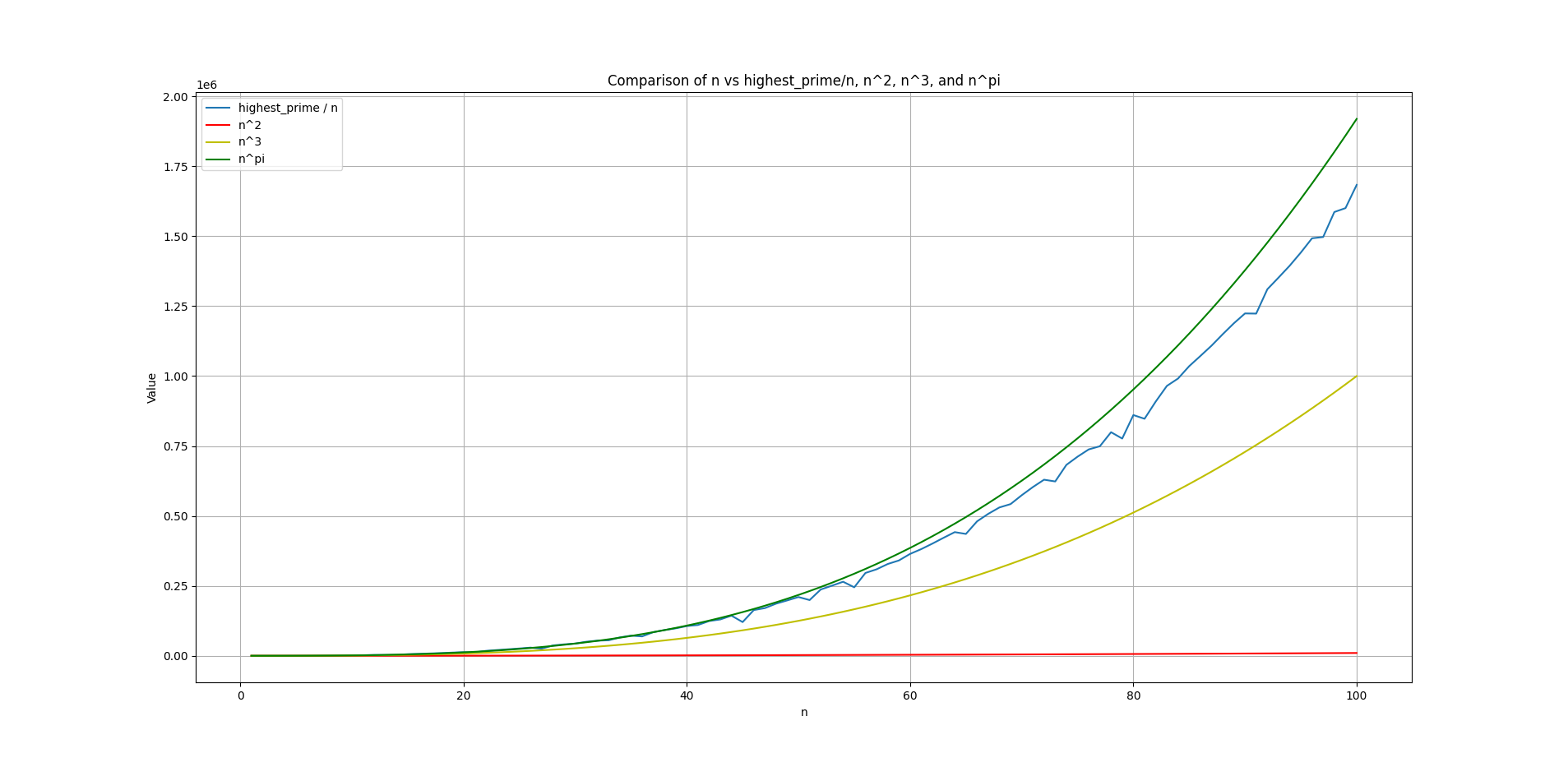For \(n = 1\) to \(n = 100\)
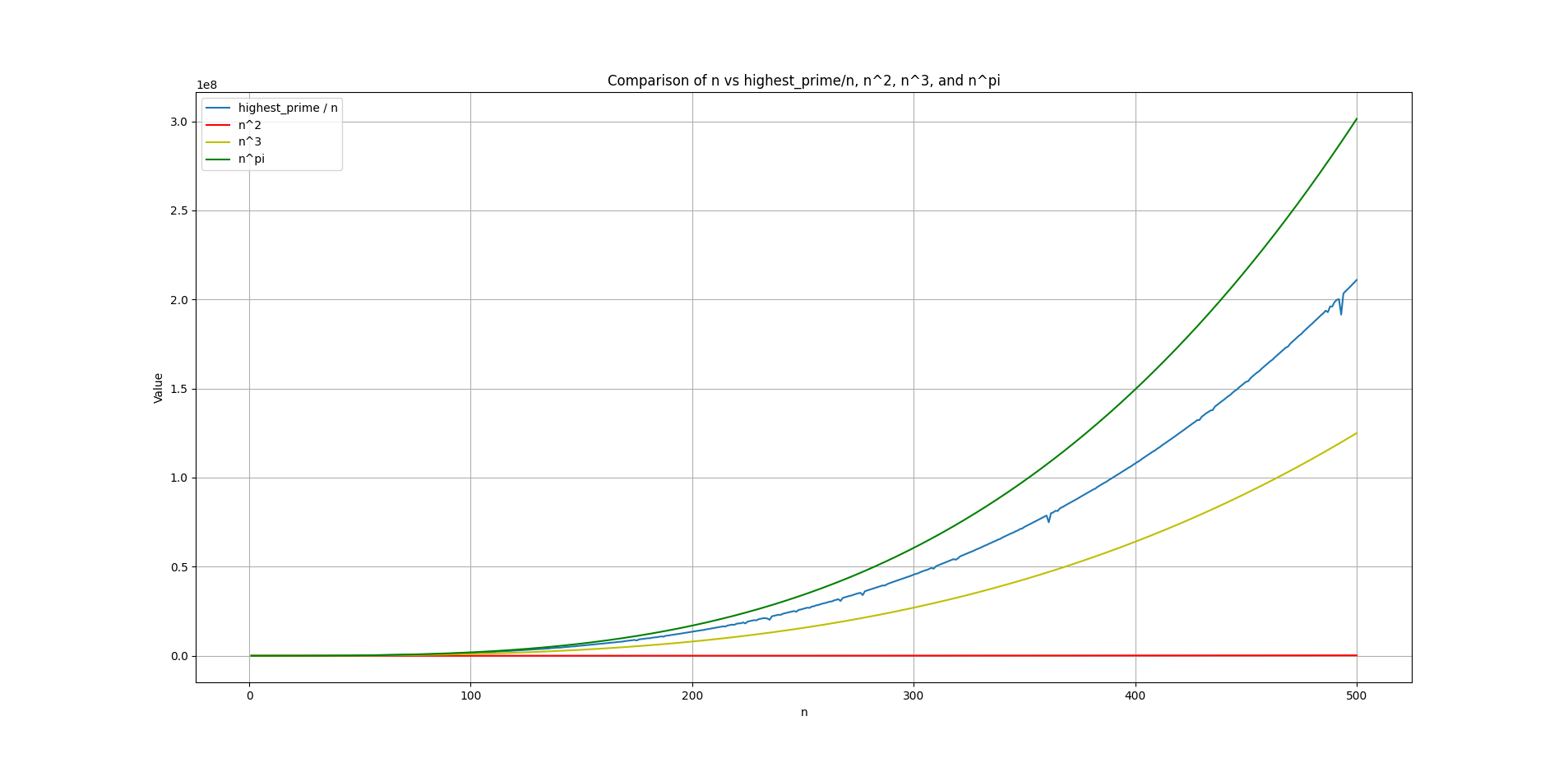For \(n = 1\) to \(n = 500\)
The script used to render this graph is as follows -
#!/usr/bin/python3
import math
import matplotlib.pyplot as plt
def is_prime(num):
if num <= 1:
return False
for i in range(2, int(math.sqrt(num)) + 1):
if num % i == 0:
return False
return True
def gcd(a, b):
while b:
a, b = b, a % b
return a
def test_conjecture(n, limit=1000):
highest_prime = 0
for a in range(1, limit + 1):
b = 2 * n - a
if gcd(a, b) == 1:
for k in [1, 2]:
expr = a**3 * b + n * k
if is_prime(expr) and expr > highest_prime:
highest_prime = expr
return highest_prime
if __name__ == "__main__":
start_n = int(input("Enter the starting value of n: "))
end_n = int(input("Enter the ending value of n: "))
n_values = list(range(start_n, end_n + 1))
highest_prime_div_n = []
for n in n_values:
highest_prime = test_conjecture(n)
if highest_prime > 0:
highest_prime_div_n.append(highest_prime / n)
else:
highest_prime_div_n.append(0)
n_squared = [n**2 for n in n_values]
n_cubed = [n**3 for n in n_values]
n_fourth = [n**3.14159265359 for n in n_values]
plt.plot(n_values, highest_prime_div_n, label="highest_prime / n")
plt.plot(n_values, n_squared, 'r', label="n^2")
plt.plot(n_values, n_cubed, 'y', label="n^3")
plt.plot(n_values, n_fourth, 'g', label="n^pi")
plt.xlabel('n')
plt.ylabel('Value')
plt.title('Comparison of n vs highest_prime/n, n^2, n^3, and n^pi')
plt.legend()
plt.grid()
plt.show()
The essence of this conjecture :
So what’s the essence of this conjecture you may ask? why are we doing this even?
Few things to realize is that - we have a polynomial which is guided by the constraint that \(2n = a+ b\) yields a finite pair of \((a,b)\) which we have to test against the expression in hand. It’s not much, it’ll always be limited and finite numbers to conduct a primality test against. We can also make some filtering to reduce the number of obvious “False positives” and then trim down to some handful of numbers. This conjecture however doesn’t promise that it’s expression will yield and range over almost / all the primes in existence, unlike the Generalize Goldbach’s conjecture, because this polynomial is of very special form in itself. But it aims to shoot higher at the primes and yields much bigger ones, potentially it will aim at those primes which are separated by much larger gaps between them.
When \(n = 10,00,000\) (a Million), the highest prime it yields is 1,957,321,022,369,599 which is 1,957,320,000 times bigger than a Million. Think about it.
And if you’re thinking - hmmm… that’s alright… BUT Can we go bigger with much smaller n ?!
I’ve heard you!
I have devised a polynomial which for \(n = 80\) yields the highest prime as - 1,852,428,239,144,333 and for \(n = 81\) yields 2,048,125,793,109,769 which has already surpassed the above one. Holy smokes, we have dropped from using 1 Million for the value of \(n\) to just 81 now! And for \(n = 100\) it yields the highest prime as 10,595,396,907,815,807
For n = 80, highest prime = 1852428239144333 with a = 66 and b = 94.
For n = 81, highest prime = 2048125793109769 with a = 66 and b = 96.
For n = 100, highest prime = 10595396907815807 with a = 93 and b = 107.
For n = 150, highest prime = 283402335267592921 with a = 119 and b = 181.
For n = 200, highest prime = 2788987275003113651 with a = 145 and b = 255.
Now you can imagine why my laptop was heating up pretty quick and easy when \(n\) was equal to 1 Million for this very polynomial, It ain’t happening on my end at least, I need access to much powerful computers.
But mind you - this was a prototype which I devised on the fly. So, consistency in its results might not be something I would vouch for. Essentially what we are saying is - “There are certain prime numbers which could be expressed in the form of this specific polynomial, under certain conditions”. Therefore, more closer we stick to the abstract forms of representing prime numbers in the forms of squares, cubes and other primes, more consistent results we’ll get. So majority of my proposed conjectures convey more or less the same message. Polynomials and Conjectures like these are a beautiful blend of imagination, creativity and the essence of representing primes in different forms.
The prototype expression which yields such bigger primes is - \(a^3 + b^2 + a^2 * b^3 * n^3 + 1\). The statement of proposed expression would go like this - (I have tested it and it fails for some initial inputs like \(n = 1,3,5,6,7\) etc but it’s almost consistent afterwards) :
For every \(2n = a + b\) where \(n \in N\), there always exists minimum one pair \((a,b)\) such that \(a^3 + b^2 + a^2 * b^3 * n^3 + 1\) is prime.
This is not a conjecture per se, but rather a big prime number generating polynomial. I am pretty sure if we made several other complex prototyes that would potentially yield much bigger primes, but for the sake of consistency and cost-effectiveness, we should stick to the core polynomial forms proposed earlier. We shouldn’t over complicate the polynomials, until unless needed.
Here’s the script used in testing it -
#!/usr/bin/python3
import math
from tabulate import tabulate
def is_prime(num):
if num <= 1:
return False
for i in range(2, int(math.sqrt(num)) + 1):
if num % i == 0:
return False
return True
def test_conjecture(n, limit=1000):
highest_prime = 0
best_a, best_b = None, None
for a in range(1, limit + 1):
b = 2 * n - a
expr = a**3 + b**2 + a**2 * b**3 * n**3 + 1
if is_prime(expr) and expr > highest_prime:
highest_prime = expr
best_a, best_b = a, b
return highest_prime, best_a, best_b
if __name__ == "__main__":
start_n = int(input("Enter the starting value of n: "))
end_n = int(input("Enter the ending value of n: "))
n_values = list(range(start_n, end_n + 1))
results = [test_conjecture(n) for n in n_values]
table_data = [(n, highest_prime) for n, (highest_prime, _, _) in zip(n_values, results)]
headers = ["n", "Highest Prime"]
print(tabulate(table_data, headers=headers, tablefmt="grid"))
print("\nCalculation steps:")
for n, (highest_prime, a, b) in zip(n_values, results):
if a is not None and b is not None:
print(f"For n = {n}, highest prime = {highest_prime} with a = {a} and b = {b}.")
else:
print(f"For n = {n}, no prime found.")
Like I said, it was a prototype, but this script was intended for some other polynomial : \(a^3 + b^2 +1\), it grew pretty fast but couldn’t compete against the \(a^3b +nk\), So I am happy I made something even more powerful. These polynomials not only generate bigger primes, but they do it in volumes, as \(n\) grows.
Prime Entanglement
Two different expressions being primes simultaneously, that’s all it is about!
You might have noticed that from Conjecture 1 to 1.3 in the previous blog, there was segment which said - such that both expression_1 and expression_2 are Primes simultaneously. I have plenty of similar proposed conjectures and prototypes, but here I will showcase one of them -
For every \(2n = a + b\) where \(n \in N\) and \(n > 1\), there always exists minimum one pair \((a,b)\) such that both \(a + n\) and \(3n + b\) are primes simultaneously.
Here’s the script used to test it -
#!/usr/bin/python3
import sympy
def is_prime(n):
return sympy.isprime(n)
def test_conjecture(n_start, n_end):
for n in range(n_start, n_end + 1):
found_pairs = []
for a in range(1, 2 * n):
b = 2 * n - a
if is_prime(3 * n + b) and is_prime(a + n):
found_pairs.append((a, b, 3 * n + b, a + n))
if found_pairs:
print(f"For n = {n}, found pairs:")
for pair in found_pairs:
print(f"a = {pair[0]}, b = {pair[1]}, 3n+b = {pair[2]}, a+n = {pair[3]}")
else:
print(f"No pairs found for n = {n}")
return False
return True
n_start = int(input("Enter the starting value of n (greater than 1): "))
n_end = int(input("Enter the ending value of n: "))
if n_start <= 1:
print("Starting value of n must be greater than 1.")
else:
result = test_conjecture(n_start, n_end)
if result:
print("Conjecture holds true for the given range of n values.")
else:
print("Conjecture doesn't hold true for the given range of n values.")
You can enter any arbitrary range of \(n\) and test it. Also the two expressions \(2n + a\) and \(2n + b\) depict the same behaviour. Thing to consider is - we can pick up some two or more distinct polynomials and since they all have the same origins (\(2n = a + b\)), we might come under impression that sticking / pairing them up might be the same thing afterall?! Eventually they’ll be primes simultaneously. But, that’s not the truth, all of these polynomials and expressions act differently.
The beauty is such - we can be assured there’s a good proportion of primes which when we find : Implies that the other expression might yield us prime as well. This Prime Entanglement theme is in it’s baby stage, but think about complex and big prime yielding polynomials in action here. It would be amazing, almost guaranteed to have primes by our side. It could also be a novel way to prove the infinitude of Twin Primes via \(2n + a\) and \(2n + b\) form.
If you wish to test the conjecture with \(2n + a\) and \(2n + b\) being primes simultaneously with \(gcd(a,b)=1\), try this script -
#!/usr/bin/python3
import math
def is_prime(n):
if n < 2:
return False
for i in range(2, math.isqrt(n) + 1):
if n % i == 0:
return False
return True
def gcd(a, b):
while b:
a, b = b, a % b
return a
def find_pairs(n):
pairs = []
for a in range(1, n+1):
b = 2 * n - a
if gcd(a, b) == 1:
pairs.append((a, b))
return pairs
def find_prime_pairs(n, pairs):
prime_pairs = []
for a, b in pairs:
y1, y2 = 2 * n + a, 2 * n + b
if is_prime(y1) and is_prime(y2):
prime_pairs.append((a, b, y1, y2))
return prime_pairs
start_n = int(input("Enter the start value for n: "))
end_n = int(input("Enter the end value for n: "))
for n in range(start_n, end_n + 1):
pairs = find_pairs(n)
prime_pairs = find_prime_pairs(n, pairs)
if prime_pairs:
print(f"For n = {n}:")
for prime_pair in prime_pairs:
a, b, y1, y2 = prime_pair
print(f" Found pair (a, b): ({a}, {b}), with 2n + a: {y1} and 2n + b: {y2}.")
else:
print(f"No prime pairs found for n = {n}.")
And notice how close the Primes with gap of 2 emerge frequently.
Squares, Cubes and Primes
Remember in the previous blog there was Conjecture 6 which said -
In general, square of any natural number (\(n^2\)) can be expressed as sum or difference of some perfect cube (\(a^3\)) with some prime number (\(p\)).
\[n^2 = a^3 \pm p\]Now, I have tested this conjecture for first 1 Million natural numbers. And, this script which ChatGPT-4 gave, has not been able to find the cubes and prime for some numbers which are -
Couldn't find a cube and a prime number that add or subtract to the square of :
64 (4096).
216 (46656).
1000 (1000000).
1331 (1771561).
1728 (2985984).
2197 (4826809).
4096 (16777216).
5832 (34012224).
6859 (47045881).
10648 (113379904).
15625 (244140625).
19683 (387420489).
24389 (594823321).
35937 (1291467969).
39304 (1544804416).
59319 (3518743761).
68921 (4750104241).
74088 (5489031744).
85184 (7256313856).
91125 (8303765625).
97336 (9474296896).
103823 (10779215329).
132651 (17596287801).
140608 (19770609664).
148877 (22164361129).
166375 (27680640625).
205379 (42180533641).
216000 (46656000000).
226981 (51520374361).
238328 (56800235584).
250047 (62523502209).
262144 (68719476736).
274625 (75418890625).
314432 (98867482624).
373248 (139314069504).
405224 (164206490176).
421875 (177978515625).
438976 (192699928576).
456533 (208422380089).
474552 (225199600704).
512000 (262144000000).
551368 (304006671424).
571787 (326940373369).
658503 (433626201009).
704969 (496981290961).
729000 (531441000000).
778688 (606355001344).
884736 (782757789696).
970299 (941480149401).
So, Under a million there are just 49 of them (And, none of them are Primes). It’s almost impossible to disprove or discredit the conjecture at this point until unless we have exhausted the set of infinity in search of such sum or difference, or perhaps when mathematically disproven for specially these numbers. This would require much more bigger cubes to try our hands on and with bigger primes, it’s a game of sum or difference afterall, and since these numbers are massive in themselves we can expect that.
Here’s the script to test this conjecture -
#!/usr/bin/python3
import sympy
def find_cube_and_prime(num):
i = 1
while True:
cube = i ** 3
if cube > num * 1000000: # Increase this value if you want to search more extensively
break
if sympy.isprime(num - cube):
return cube, num - cube
if sympy.isprime(cube - num):
return cube, -(cube - num)
i += 1
return None, None
# Take user input for the range
start = int(input("Enter the start of the range: "))
end = int(input("Enter the end of the range: "))
for number in range(start, end + 1):
squared_number = number ** 2
cube, prime = find_cube_and_prime(squared_number)
if cube and prime:
if prime > 0:
print(f"{squared_number} (square of {number}) can be expressed as the sum of {cube} and {prime}.")
else:
print(f"{squared_number} (square of {number}) can be expressed as the difference of {cube} and {-prime}.")
else:
print(f"Couldn't find a cube and a prime number that add or subtract to the square of {number} ({squared_number}).")
Key thing to note here is that - The resulting pairs of \(a^3\) and \(p\) is not the only possible combination, because this script works in a certain way, it moves on to other numbers in the list to try.
Mystery of Common Exceptions
Consider these two conjectures again -
For every \(2n = a + b\) where \(n \in N\), there always exists minimum one pair \((a,b)\) such that \(2(a+n) + ab\) is prime.
EXCEPTION : \(2n=42\)
For every \(2n = a + b\) where \(n \in N\), there always exists minimum one pair \((a,b)\) with \(gcd(a,b)=1\) such that \(n^2 + n + (ab+2)\) is prime.
EXCEPTION : \(2n=42\)
First of all, these two are not the only ones which threw exception(s) - tested till 1 Million, and in the previous blog I hadn’t mentioned others, which I am listing below. It’s something I can’t explain in words. This phenomenon in itself is a great mystery to me. We can certainly explain the how? of these exceptions, but why? is something we should strive for. Whether I am ignorant about any branch of mathematics which works this intimate with the relationship between polynomials and primes or there is serious need to have a new realm of mathematics which helps us better understand these patterns in prime numbers.
Below are the scripts for testing these two conjectures in their subsequent order -
\[2(a + n) + ab\]#!/usr/bin/python3
import math
def is_prime(num):
if num <= 1:
return False
for i in range(2, int(math.sqrt(num)) + 1):
if num % i == 0:
return False
return True
def test_conjecture(n):
prime_pairs = []
for a in range(1, 2 * n):
b = 2 * n - a
expression = 2 * (a + n) + a * b
if is_prime(expression):
prime_pairs.append((a, b, expression))
return prime_pairs
def main():
start_n = int(input("Enter the starting value of n: "))
end_n = int(input("Enter the ending value of n: "))
for n in range(start_n, end_n+1):
prime_pairs = test_conjecture(n)
if prime_pairs:
print(f"For n = {n}, the following pairs of (a, b) make the expression prime:")
for a, b, prime in prime_pairs:
print(f"a = {a}, b = {b}, prime = {prime}")
else:
print(f"The conjecture does not hold for n = {n}")
if __name__ == "__main__":
main()
#!/usr/bin/python3
import math
def is_prime(num):
if num < 2:
return False
for i in range(2, int(num**0.5) + 1):
if num % i == 0:
return False
return True
def generate_pairs(n):
pairs = []
for a in range(1, 2 * n):
b = 2 * n - a
if math.gcd(a, b) == 1:
pairs.append((a, b))
return pairs
def find_prime_pairs(n):
prime_pairs = []
pairs = generate_pairs(n)
for a, b in pairs:
expression = n**2 + n + (a * b + 2)
if is_prime(expression):
prime_pairs.append((a, b, expression))
return prime_pairs
def main():
start_n = int(input("Enter the starting value of n: "))
end_n = int(input("Enter the ending value of n: "))
for n in range(start_n, end_n + 1):
prime_pairs = find_prime_pairs(n)
if prime_pairs:
print(f"Prime pairs and the primes they generate for n = {n}:")
lowest_prime = float('inf')
highest_prime = float('-inf')
for a, b, prime in prime_pairs:
print(f"a = {a}, b = {b}, prime = {prime}")
if prime < lowest_prime:
lowest_prime = prime
if prime > highest_prime:
highest_prime = prime
print(f"Lowest prime: {lowest_prime}")
print(f"Highest prime: {highest_prime}")
else:
print(f"No prime pairs found for n = {n}")
if __name__ == "__main__":
main()
Other similar polynomials with known Exception(s)
For every \(2n = a + b\) where \(n \in N\), there always exists minimum one pair \((a,b)\) with \(gcd(a,b)=1\) such that \(an +b(n+1)^2\) is prime.
EXCEPTION : \(2n=10\)
For every \(2n = a + b\) where \(n \in N\), there always exists minimum one pair \((a,b)\) such that \(b^3 - a^2 + 5ab\) is prime.
EXCEPTION : \(2n=112\) and \(1456\)
For every \(2n = a + b\) where \(n \in N\), there always exists minimum one pair \((a,b)\) such that \(a^3 + b^2 + 1\) is prime.
EXCEPTION : \(2n=12\) and \(48\)
Charting the Course Forward
I have some polynomials by my side, which are insanely interesting, at least to me. Some fall into the category of evading gaps in Prime number’s distribution. Some just result in numbers which are either prime themselves or they are nearby some primes, as \(n\) grows, so does the margin by \(2n\) since primes have even gaps between them. Like you’ve witnessed expressions which result in being primes simultaneously, then there are expressions which make a range, say between 20 and 30 and suggest how many primes you’ll get between that range as \(n\) grows and so on…
I am not actively working on these conjectures, last time I worked was in late 2019. Hope this blog post reflects some deep insights into these proposed conjectures. If you wish to discuss with me any further, consider emailing me at [email protected].
or Contact me here.
Thank you so much for giving it a read!